Bất Phương Trình Mũ Và Logarit

Mô tả sản phẩm

Bất phương trình mũ và logarit là những bất phương trình có chứa hàm mũ và hàm logarit. Giải quyết chúng đòi hỏi sự hiểu biết về tính chất của các hàm này và kỹ thuật biến đổi tương đương để đưa về dạng dễ giải hơn. Bài viết này sẽ hướng dẫn bạn cách giải các loại bất phương trình này một cách chi tiết và hiệu quả.

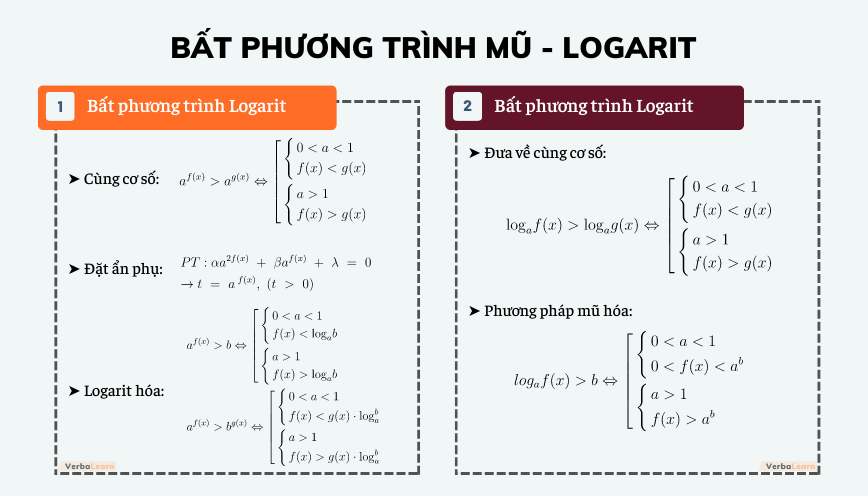
Các dạng bất phương trình mũ và logarit thường gặp

Bất phương trình mũ cơ bản:

Giải bất phương trình mũ cơ bản thường liên quan đến việc so sánh hai lũy thừa cùng cơ số hoặc biến đổi về dạng cùng cơ số. Ví dụ: 2^x > 8 tương đương với 2^x > 2³, từ đó suy ra x > 3. Những trường hợp phức tạp hơn có thể cần dùng đến phép biến đổi logarit để giải.

Bất phương trình logarit cơ bản:

Tương tự, bất phương trình logarit cơ bản thường liên quan đến việc so sánh hai logarit cùng cơ số. Ví dụ: log₂x > 3 tương đương với x > 2³ = 8 (với điều kiện x > 0). Việc xét điều kiện xác định của logarit là rất quan trọng trong việc giải bất phương trình logarit.

Bất phương trình mũ và logarit phức tạp:

Các bất phương trình phức tạp hơn có thể bao gồm nhiều hàm mũ và logarit, các phép toán cộng, trừ, nhân, chia, hoặc các hàm khác. Để giải những bất phương trình này, ta cần sử dụng các kỹ thuật biến đổi như: đặt ẩn phụ, sử dụng tính chất của hàm mũ và logarit, vẽ đồ thị, khảo sát hàm số… Một số trường hợp cần đến sự trợ giúp của máy tính để tìm nghiệm gần đúng.

Kỹ thuật giải bất phương trình mũ và logarit

Đặt ẩn phụ:

Trong nhiều trường hợp, đặt ẩn phụ giúp đơn giản hóa bất phương trình và đưa về dạng dễ giải hơn. Ví dụ: 3^2x + 3^x - 2 > 0 có thể đặt t = 3^x (t > 0) để đưa về phương trình bậc hai t² + t - 2 > 0.

Sử dụng tính chất của hàm mũ và logarit:

Việc hiểu rõ tính chất đơn điệu của hàm mũ và logarit là rất quan trọng. Ví dụ, nếu cơ số a > 1 thì hàm y = a^x đồng biến, còn nếu 0 < a < 1 thì hàm y = a^x nghịch biến. Tương tự, nếu cơ số a > 1 thì hàm y = log_ax đồng biến, còn nếu 0 < a < 1 thì hàm y = log_ax nghịch biến. Việc sử dụng tính chất này giúp ta dễ dàng so sánh các giá trị và tìm nghiệm của bất phương trình.

Vẽ đồ thị:

Vẽ đồ thị hàm số có thể giúp ta trực quan hóa bất phương trình và tìm nghiệm một cách nhanh chóng. Tuy nhiên, phương pháp này chỉ hiệu quả với các bất phương trình đơn giản.

Khảo sát hàm số:

Đối với các bất phương trình phức tạp, việc khảo sát hàm số có thể giúp ta xác định khoảng nghiệm của bất phương trình. Phương pháp này đòi hỏi kiến thức sâu rộng về giải tích.

Sản phẩm liên quan: các dạng bài tập ma trận và cách giải

Sản phẩm liên quan: cách xác định phương thức biểu đạt

Sản phẩm liên quan: số electron tối đa trong lớp m là