Bất Đẳng Thức Trong Tam Giác

Mô tả sản phẩm

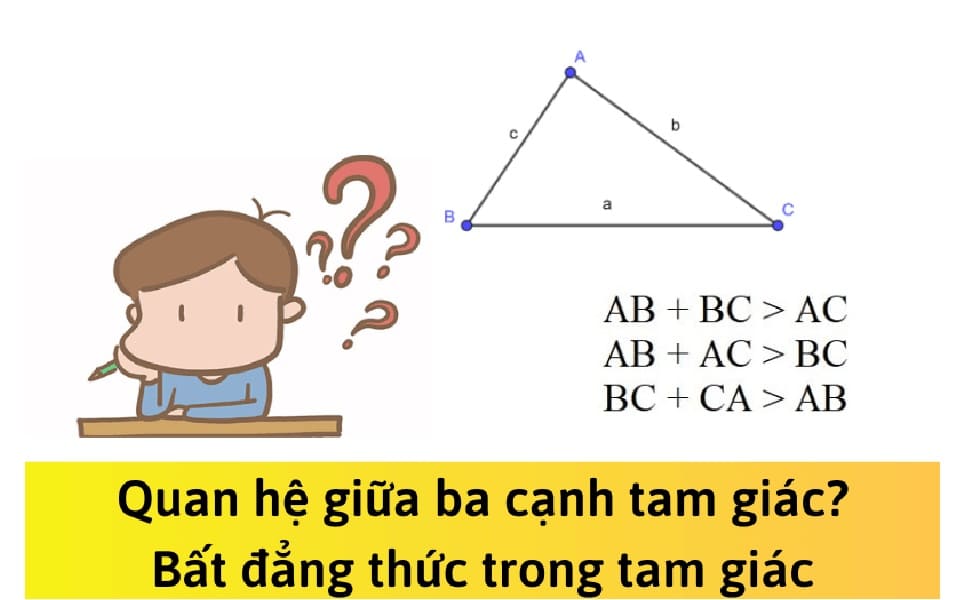
Bất đẳng thức trong tam giác khẳng định rằng tổng độ dài hai cạnh bất kỳ của một tam giác luôn lớn hơn độ dài cạnh còn lại. Đây là một định lý cơ bản và quan trọng trong hình học, được sử dụng rộng rãi để giải quyết các bài toán liên quan đến tam giác.

Khái niệm và Định lý

Định lý cơ bản:

Trong một tam giác ABC với độ dài ba cạnh a, b, c (a đối diện với góc A, b đối diện với góc B, c đối diện với góc C), ta có các bất đẳng thức sau:

• a + b > c
• a + c > b
• b + c > a

Điều này có nghĩa là tổng độ dài của hai cạnh bất kỳ luôn lớn hơn độ dài cạnh còn lại. Nếu bất đẳng thức nào không được thỏa mãn, thì ba độ dài đó không thể tạo thành một tam giác.

Ứng dụng của bất đẳng thức tam giác

Trong giải toán hình học:

Bất đẳng thức tam giác được ứng dụng rộng rãi để chứng minh các tính chất hình học, giải các bài toán liên quan đến độ dài cạnh, bất đẳng thức tam giác giúp ta xác định xem ba đoạn thẳng có thể tạo thành một tam giác hay không. Nó cũng là công cụ quan trọng trong việc tìm ra khoảng cách ngắn nhất giữa hai điểm, hay tìm vị trí của một điểm thỏa mãn điều kiện nào đó.

Trong các lĩnh vực khác:

Ngoài hình học, bất đẳng thức tam giác cũng xuất hiện trong nhiều lĩnh vực khác như vật lý, tin học, và toán học ứng dụng. Ví dụ, trong tin học, nó được sử dụng trong thuật toán tìm đường ngắn nhất (như thuật toán Dijkstra).

Ví dụ minh họa

Ví dụ 1:

Cho ba đoạn thẳng có độ dài 2, 3, 6. Kiểm tra xem ba đoạn thẳng này có thể tạo thành một tam giác hay không. Ta kiểm tra các bất đẳng thức:

• 2 + 3 > 6 (Sai)

Vì bất đẳng thức không được thỏa mãn, nên ba đoạn thẳng này không thể tạo thành một tam giác.

Ví dụ 2:

Cho tam giác ABC có AB = 5, AC = 7. Tìm khoảng giá trị có thể có của BC. Theo bất đẳng thức tam giác, ta có:

• BC < AB + AC = 5 + 7 = 12
• BC > |AB - AC| = |5 - 7| = 2

Vậy 2 < BC < 12.

Xem thêm: keo xám dán ron

Xem thêm: ví shopee pay la gì

Xem thêm: vẽ biểu đồ lực dọc