Bảng Đạo Hàm Loga
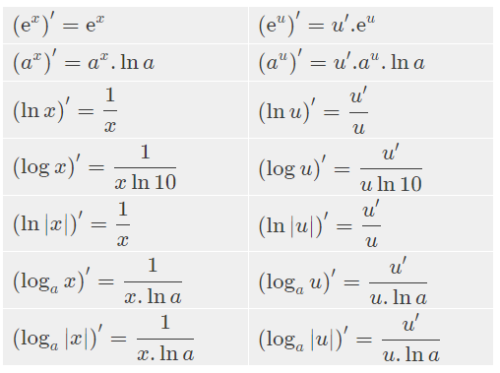

Chính Sách Vận Chuyển Và Đổi Trả Hàng
Miễn phí vận chuyển mọi đơn hàng từ 500K
- Phí ship mặc trong nước 50K
- Thời gian nhận hàng 2-3 ngày trong tuần
- Giao hàng hỏa tốc trong 24h
- Hoàn trả hàng trong 30 ngày nếu không hài lòng
Mô tả sản phẩm
Bảng đạo hàm logarit dưới đây cung cấp công thức đạo hàm của các hàm logarit cơ bản và mở rộng, giúp bạn dễ dàng tính toán đạo hàm trong các bài toán giải tích.
Công thức đạo hàm logarit cơ bản
Đạo hàm của hàm logarit tự nhiên (ln x)
Đạo hàm của hàm logarit tự nhiên ln(x) là 1/x. Công thức cụ thể như sau:
d(ln x)/dx = 1/x (với x > 0)
Đạo hàm của hàm logarit cơ số a (loga x)
Đạo hàm của hàm logarit cơ số a, loga(x), được tính theo công thức:
d(loga x)/dx = 1/(x ln a) (với x > 0 và a > 0, a ≠ 1)
Đạo hàm của hàm hợp logarit
Nếu có hàm hợp dạng y = ln(u(x)) hoặc y = loga(u(x)), thì đạo hàm được tính theo quy tắc chuỗi:
d(ln(u(x)))/dx = u'(x)/u(x)
d(loga(u(x)))/dx = u'(x)/(u(x)ln a)
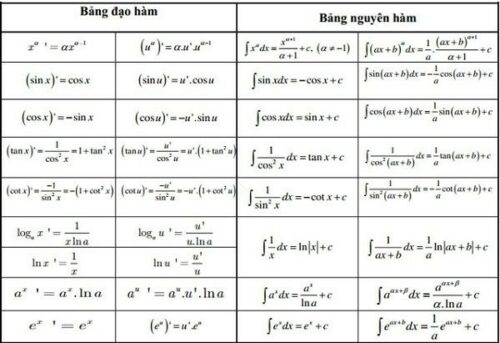
Bảng tóm tắt các công thức đạo hàm logarit
Dưới đây là bảng tóm tắt các công thức đạo hàm logarit quan trọng:
| Hàm số | Đạo hàm | Điều kiện |
|---|---|---|
| ln x | 1/x | x > 0 |
| loga x | 1/(x ln a) | x > 0, a > 0, a ≠ 1 |
| ln(u(x)) | u'(x)/u(x) | u(x) > 0 |
| loga(u(x)) | u'(x)/(u(x)ln a) | u(x) > 0, a > 0, a ≠ 1 |
Lưu ý: Các công thức trên áp dụng cho các hàm logarit xác định. Luôn kiểm tra điều kiện xác định của hàm số trước khi tính đạo hàm.
Sản phẩm liên quan: phân tích bài thơ lời ru của mẹ
Sản phẩm hữu ích: khtn lớp 7 chân trời sáng tạo
Sản phẩm liên quan: cây đa chú cuội
Sản phẩm hữu ích: tính n trong hóa học
Sản phẩm liên quan: say sưa hay say xưa