Bán kính mặt cầu ngoại tiếp tứ diện đều

Mô tả sản phẩm

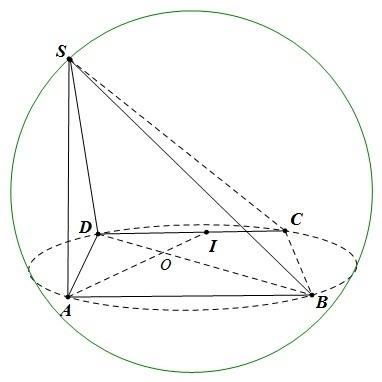
Bán kính mặt cầu ngoại tiếp tứ diện đều cạnh a bằng a√6 / 4.

Công thức tính bán kính mặt cầu ngoại tiếp tứ diện đều

Từ định nghĩa

Tứ diện đều là một hình tứ diện có tất cả các cạnh bằng nhau. Mặt cầu ngoại tiếp tứ diện đều là mặt cầu đi qua tất cả bốn đỉnh của tứ diện. Để tính bán kính mặt cầu này, ta cần xác định tâm và khoảng cách từ tâm đến mỗi đỉnh (bán kính). Tâm của mặt cầu ngoại tiếp tứ diện đều chính là trọng tâm của tứ diện. Bằng cách sử dụng các công thức hình học không gian và tính chất đặc biệt của tứ diện đều, ta suy ra được công thức bán kính R như trên.

Từ mối liên hệ với cạnh

Công thức R = a√6 / 4 cho thấy bán kính mặt cầu ngoại tiếp tứ diện đều phụ thuộc trực tiếp vào độ dài cạnh a của tứ diện. Nếu biết độ dài cạnh a, ta có thể dễ dàng tính được bán kính R. Đây là một công thức quan trọng trong hình học không gian và thường được sử dụng trong các bài toán liên quan đến tứ diện đều và mặt cầu.

Ví dụ minh họa

Giả sử ta có một tứ diện đều với cạnh a = 2cm. Áp dụng công thức, bán kính mặt cầu ngoại tiếp tứ diện này là: R = 2√6 / 4 = √6 / 2 ≈ 1.22 cm.

Ứng dụng của công thức

Công thức tính bán kính mặt cầu ngoại tiếp tứ diện đều có nhiều ứng dụng trong các lĩnh vực khác nhau, ví dụ như:

• Xác định kích thước của các cấu trúc tinh thể.
• Tính toán thể tích của các vật thể hình học.
• Giải quyết các bài toán hình học không gian phức tạp.

Sản phẩm liên quan: gang có tính chất gì

Sản phẩm hữu ích: chất nào là chất tinh khiết

Sản phẩm liên quan: tác dụng phụ của hoa đậu biếc

Sản phẩm hữu ích: cách tính phần trăm của một số

Sản phẩm hữu ích: công suất w là gì