Bài tập tính độ lệch chuẩn

Mô tả sản phẩm

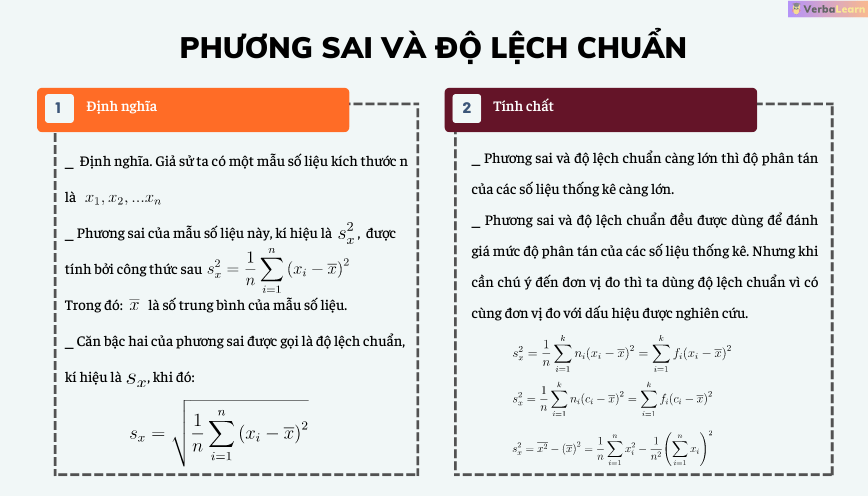
Bài viết này sẽ hướng dẫn bạn cách tính độ lệch chuẩn, một chỉ số thống kê quan trọng giúp đo lường mức độ phân tán của dữ liệu so với giá trị trung bình. Bạn sẽ tìm thấy các ví dụ cụ thể và bước thực hiện chi tiết để hiểu rõ hơn về khái niệm này.

Cách tính độ lệch chuẩn

Bước 1: Tính giá trị trung bình (x̄)

Đầu tiên, bạn cần tính giá trị trung bình của tập dữ liệu. Công thức tính giá trị trung bình là: x̄ = (Σx) / n, trong đó Σx là tổng các giá trị trong tập dữ liệu và n là số lượng giá trị.

Bước 2: Tính độ lệch của mỗi giá trị so với trung bình (x - x̄)

Tiếp theo, hãy tính độ lệch của mỗi giá trị trong tập dữ liệu so với giá trị trung bình đã tính ở bước 1. Kết quả có thể là số dương hoặc số âm.

Bước 3: Bình phương các độ lệch (x - x̄)²

Bình phương mỗi độ lệch đã tính ở bước 2 để loại bỏ dấu âm và nhấn mạnh các giá trị lệch xa trung bình.

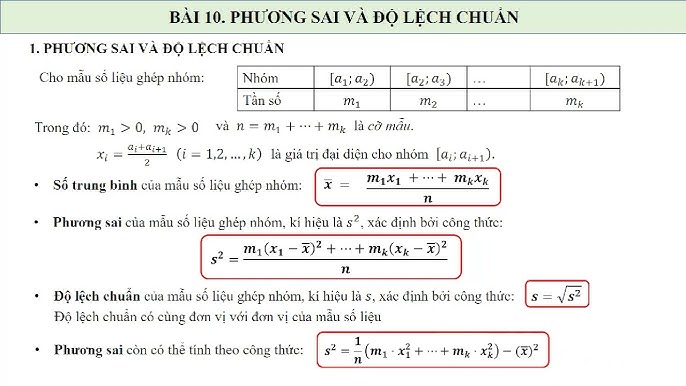
Bước 4: Tính phương sai (s²)

Phương sai là trung bình bình phương các độ lệch. Công thức tính phương sai là: s² = Σ(x - x̄)² / (n - 1) (sử dụng n-1 cho mẫu, n cho toàn bộ quần thể).

Bước 5: Tính độ lệch chuẩn (s)

Độ lệch chuẩn là căn bậc hai của phương sai. Công thức tính độ lệch chuẩn là: s = √s²

Ví dụ minh họa

Giả sử chúng ta có tập dữ liệu sau: {2, 4, 6, 8, 10}. Hãy cùng thực hiện các bước trên để tính độ lệch chuẩn:

Bước 1: Tính trung bình

x̄ = (2 + 4 + 6 + 8 + 10) / 5 = 6

Bước 2 & 3: Tính độ lệch và bình phương

(2 - 6)² = 16
(4 - 6)² = 4
(6 - 6)² = 0
(8 - 6)² = 4
(10 - 6)² = 16

Bước 4: Tính phương sai

s² = (16 + 4 + 0 + 4 + 16) / (5 - 1) = 10

Bước 5: Tính độ lệch chuẩn

s = √10 ≈ 3.16

Vậy độ lệch chuẩn của tập dữ liệu này là khoảng 3.16.

Kết luận

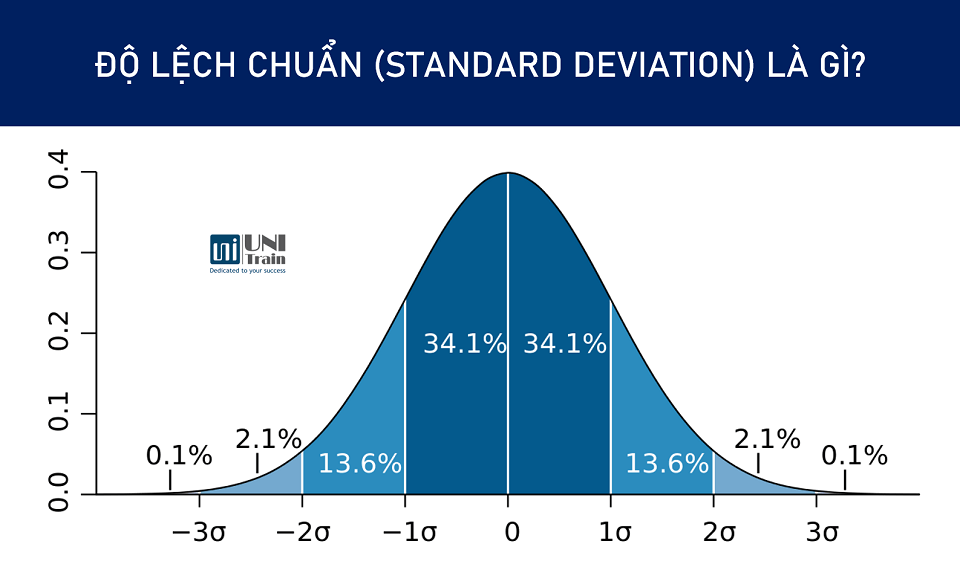
Hiểu cách tính độ lệch chuẩn giúp bạn phân tích dữ liệu hiệu quả hơn. Độ lệch chuẩn càng cao, dữ liệu càng phân tán, và ngược lại.

Sản phẩm liên quan: an ủi bao nhiêu tiền

Sản phẩm hữu ích: mắt có cấu tạo như thế nào

Sản phẩm liên quan: trong các phát biểu về mạng máy tính sau phát biểu nào đúng

Sản phẩm hữu ích: cách tạo thư mục trên máy tính

Sản phẩm liên quan: hàm tìm giá trị trong khoảng