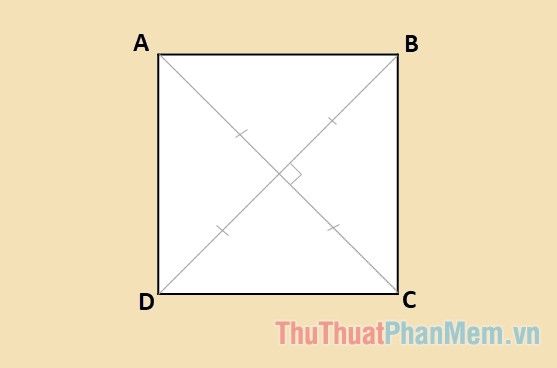
Hai đường chéo hình vuông có vuông góc không?

Mô tả sản phẩm

Câu trả lời ngắn gọn là: Có, hai đường chéo của hình vuông luôn vuông góc với nhau.

Chứng minh hai đường chéo hình vuông vuông góc

Tính chất hình vuông

Hình vuông là một tứ giác đặc biệt, hội tụ đầy đủ các tính chất của hình chữ nhật, hình thoi và hình thang cân. Cụ thể, hình vuông có các cạnh bằng nhau, các góc bằng nhau (đều bằng 90 độ), hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường.

Phân tích chứng minh

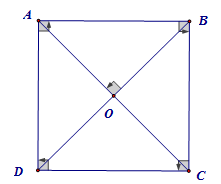
Để chứng minh hai đường chéo của hình vuông vuông góc, ta có thể sử dụng nhiều cách. Một cách đơn giản là dựa vào tính chất của hình thoi. Hình vuông cũng là một hình thoi, mà trong hình thoi, hai đường chéo vuông góc với nhau. Do đó, hai đường chéo của hình vuông cũng vuông góc với nhau. Một cách chứng minh khác là sử dụng định lý Pitago. Gọi ABCD là hình vuông với các cạnh AB=BC=CD=DA. Hai đường chéo AC và BD cắt nhau tại O. Xét tam giác ABC, ta có AB² + BC² = AC² (định lý Pitago). Tương tự, xét tam giác ABD, ta có AB² + AD² = BD². Vì AB=BC=CD=DA, nên AC² = BD², suy ra AC = BD. Vì AC và BD cắt nhau tại trung điểm O của mỗi đường, ta có OA = OB = OC = OD. Xét tam giác AOB, ta thấy OA=OB, và góc ABO = 45 độ (vì góc ABC=90 độ và OB là đường phân giác). Do đó, tam giác AOB là tam giác cân có một góc bằng 45 độ, suy ra góc AOB = 90 độ. Vậy hai đường chéo vuông góc. Tóm lại, dựa trên các tính chất hình học và các định lý toán học, ta khẳng định chắc chắn rằng hai đường chéo của hình vuông luôn vuông góc với nhau.

Xem thêm: sự phân tích ánh sáng trắng

Sản phẩm liên quan: vòi nước nối dài

Sản phẩm liên quan: nos là đơn vị gì

Sản phẩm hữu ích: trăng tròn như cái đĩa